Table of Contents
- Ray theory
- Total internal reflection
- Critical angle
- Acceptance angle
- Numerical aperture
- Skew rays
The phenomenon of splitting of white light into its constituents is known as dispersion. The concepts
of reflection and refraction of light are based on a theory known as Ray theory or geometric optics,
where light waves are considered as waves and represented with simple geometric lines or rays.
The basic laws of ray theory/geometric optics
- In a homogeneous medium, light rays are straight lines.
- Light may be absorbed or reflected
- The reflected ray lies in the plane of incidence and the angle of incidence will be equal to the angle of reflection.
- At the boundary between two media of different refractive indices, the refracted ray will lie in the plane of incidence. Snell’s Law will give the relationship between the angles of incidence and refraction.
Reflection depends on the type of surface on which light is incident. An essential condition for
reflection to occur with glossy surfaces is that the angle made by the incident ray of light with the
normal at the point of contact should be equal to the angle of reflection with that normal.
The images produced from this reflection have different properties according to the shape of the surface. For example, for a flat mirror, the image produced is upright, has the same size as that of the object and is equally distanced from the surface of the mirror as the real object. However, the
properties of a parabolic mirror are different and so on.
Refraction is the bending of light in a particular medium due to the speed of light in that medium. The v= c/n, speed of light in any medium can be given by
Refractive index (n) = Speed of Light in air/speed of light in a medium = c/n.
The refractive index for vacuum and air is 1.0 for water it is 1.3 and for glass refractive index is 1.5.
Here n is the refractive index of that medium. When a ray of light is incident at the interface of two media with different refractive indices, it will bend either towards or away from the normal depending on the refractive indices of the media.
According to Snell’s law, refraction can be represented as
n1sinθ1 = n2sinθ2
n1 = refractive index of first medium
n2 = refractive index of the second medium
i or θ1 = angle of incidence
r or θ2 = angle of refraction
For, n1> n2, θ2 is always greater than θ1. Or to put it in different words, light moving from a medium
of high refractive index (glass) to a medium of lower refractive index (air) will move away from the
normal.
To consider the propagation of light within an optical fiber utilizing the ray theory model it is
necessary to take account of the refractive index of the dielectric medium. Optical materials are
characterized by their index of refraction, referred to as n. The refractive index of a medium is defined
as the ratio of the velocity of light in a vacuum to the velocity of light in the medium. When a beam of light passes from one material to another with a different index of refraction, the
beam is bent (or refracted) at the interface
ni Sini = nr Sinr
where ni and nr are the indices of refraction of the materials through which the beam is refracted
and I and R are the angles of incidence and refraction of the beam. If the angle of incidence is greater
than the critical angle for the interface (typically about 82° for optical fibers), the light is reflected
back into the incident medium without loss by a process known as total internal reflection.
ALSO, READ OFC : Introduction
Refraction is described by Snell’s law
A ray of light travels more slowly in an optically dense medium than in one that is less dense, and the
refractive index gives a measure of this effect. When a ray is an incident on the interface between two
dielectrics of differing refractive indices (e.g. glass–air), refraction occurs. It may be observed that the ray approaching the interface is propagating in a dielectric of
refractive index n and is at an angle φ to the normal at the surface of the interface.
If the dielectric on the other side of the interface has a refractive index n which is less than n1, then
the refraction is such that the ray path in this lower index medium is at an angle to the normal, where
is greater than. The angles of incidence and refraction are related to each other and to the
refractive indices of the dielectrics by Snell’s law of refraction, which states that
n1 sinØ1 = n2 sinØ2
or
sinØ1 / sinØ2 = n2 / n1
It may also be observed in above Figure (a) that a small amount of light is reflected back into the
originating dielectric medium (partial internal reflection). As n is greater than n, the angle of
refraction is always greater than the angle of incidence. Thus when the angle of refraction is 90° and
the refracted ray emerges parallel to the interface between the dielectrics, the angle of incidence
must be less than 90°. This is the limiting case of refraction and the angle of incidence is now known as the critical angle φc,
as shown in Figure (b). The value of the critical angle is given by
sinØc = n2 / n1
At angles of incidence greater than the critical angle, the light is reflected back into the originating
dielectric medium (total internal reflection) with high efficiency (around 99.9%). Hence, it may be
observed in Figure (c) that total internal reflection occurs at the inter-face between two
dielectrics of differing refractive indices when light is incident on the dielectric of the lower index from
the dielectric of the higher index, and the angle of incidence of the ray exceeds the critical value. This is
the mechanism by which light at a sufficiently shallow angle (less than 90° − may be considered to
propagate down an optical fiber with low loss.
 |
| The transmission of a light ray in a perfect optical fiber |
The above figure illustrates the transmission of a light ray in an optical fiber via a series of total internal reflections at the interface of the silica core and the slightly lower refractive index silica cladding. The ray has an angle of incidence φ at the interface which is greater than the critical angle and is reflected at the same angle as the normal. The light ray shown in the Figure is known as a meridional ray as it passes through the axis of the fiber core. This type of ray is the simplest to describe and is generally used when illustrating the fundamental transmission properties of optical fibers. It must also be noted that the light transmission illustrated in Figure assumes a perfect fiber, and that any discontinuities or imperfections at the core-cladding interface would probably result in refraction rather than total internal reflection, with the subsequent loss of the light ray into the cladding.
When the angle of incidence (Ø1) is progressively increased, there will be a progressive increase of
refractive angle (Ø2). At some conditions (Ø1) the refractive angle (Ø2) becomes 90o
to the normal. When this
happens the refracted light ray travels along with the interface. The angle of incidence (Ø1) at the point at which the
refractive angle (Ø1) becomes 90 degrees is called the critical angle. It is denoted by Øc.
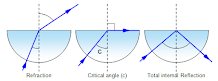
The critical angle is defined as the minimum angle of incidence (Ø1) at which the ray strikes the
interface of two media and causes an angle of refraction (Ø2) equal to 90 degrees. The below fig shows critical
angle refraction. When the angle of refraction is 90 degrees to the normal the refracted ray is parallel
to the interface between the two media.
 |
| critical angle refraction |
 |
| critical angle refraction |
Hence at critical angle Ø1 = Øc and Ø2 = 90 degrees. Using Snell’s law: n1SinØ1 = n2SinØ2
SinØc = (n2/n1) sin90
Sin90 = 1
Hence, Critical angle Øc = Sin-1(n2 / n1)
It is important to know about this property because reflection is also possible even if the surfaces
are not reflective. If the angle of incidence is greater than the critical angle for a given setting, the
resulting type of reflection is called Total Internal Reflection, and it is the basis of Optical Fiber
Communication.
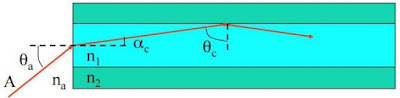
Θa)
In an optical fiber, a light ray undergoes its first refraction at the air-core interface. The angle at which
this refraction occurs is crucial because this particular angle will dictate whether the
subsequent internal reflections will follow the principle of Total Internal Reflection. This angle, at
which the light ray first encounters the core of an optical fiber is called the Acceptance angle.
Numerical Aperture is a characteristic of an optical system. For example, photo-detector, optical
fiber, lenses etc. are all-optical systems. Numerical aperture is the ability of the optical system to
collect all of the light incidents on it, in one area.
 |
| The light outside the Acceptance Cone can not be coupled onto optical fiber |
The blue cone is known as the cone of acceptance. As you can see it is dependent on the Acceptance
Angle of the optical fiber. Light waves within the acceptance cone can be collected in a small area
which can then be sent into the optical fiber (Source)
The numerical aperture (NA), shown in the above Figure, is the measure of the maximum angle at which light rays
will enter and be conducted down the fiber. This is represented by the following equation
In a multimode optical fiber, a bound ray that travels in a helical path along with the fiber and
thus (a) is not parallel to the fiber axis, (b) does not lie in a meridional plane, and (c) does not
intersect the fiber axis is known as a Skew Ray.
- Skew rays are rays that travel through an optical fiber without passing through its axis.
- A possible path of propagation of skew rays is shown in the figure. (a) provides an angled view and view (b) provides a front view.
- Skew rays are those rays that follow a helical path but are not confined to a single plane. Skew rays are not confined to a particular plane so they cannot be tracked easily. Analyzing the meridional rays is sufficient for the purpose of result, rather than skew rays because skew rays lead to greater power loss.
- Skew rays propagate without passing through the center axis of the fiber. The acceptance angle for skew rays is larger than the acceptance angle of meridional rays.
- Skew rays are often used in the calculation of light acceptance in an optical fiber. The addition of skew rays increases the amount of light capacity of a fiber. In large NA fibers, the increase may be significant.
- The addition of skew rays also increases the amount of loss in fiber. Skew rays tend to propagate near the edge of the fiber core. A large portion of the number of skew rays that are trapped in the fiber core is considered to be leaky rays.
- Leaky rays are predicted to be totally reflected at the core-cladding boundary. However, these rays are partially refracted because of the curved nature of the fiber boundary. Mode theory is also used to describe this type of leaky ray loss.










0 Comments